Marcos Lopez de Prado

I find Geometric solutions to practical Financial problems particularly powerful (here is an example). The connection between Quantitative Finance and Geometry may not be evident, however Geometry can be found at the root of fields as distant as Finance and Biology (see a connection here). Geometry allows you to formulate a problem visually and search for a solution in non-symbolic terms. How else were the Ancient Greeks able to solve complex Mathematical problems without ever using equations? Archimedes solved integral calculus questions using Geometric arguments, more than 1900 years before calculus was rediscovered by Leibniz and Newton. Gauss' first breakthrough was as a Geometer, and I suspect that the reason why Gauss' personal diaries are devoid of motivation is partly because he first approached problems Geometrically (like a Greek mathematician), and knew exactly where the arguments were leading him.

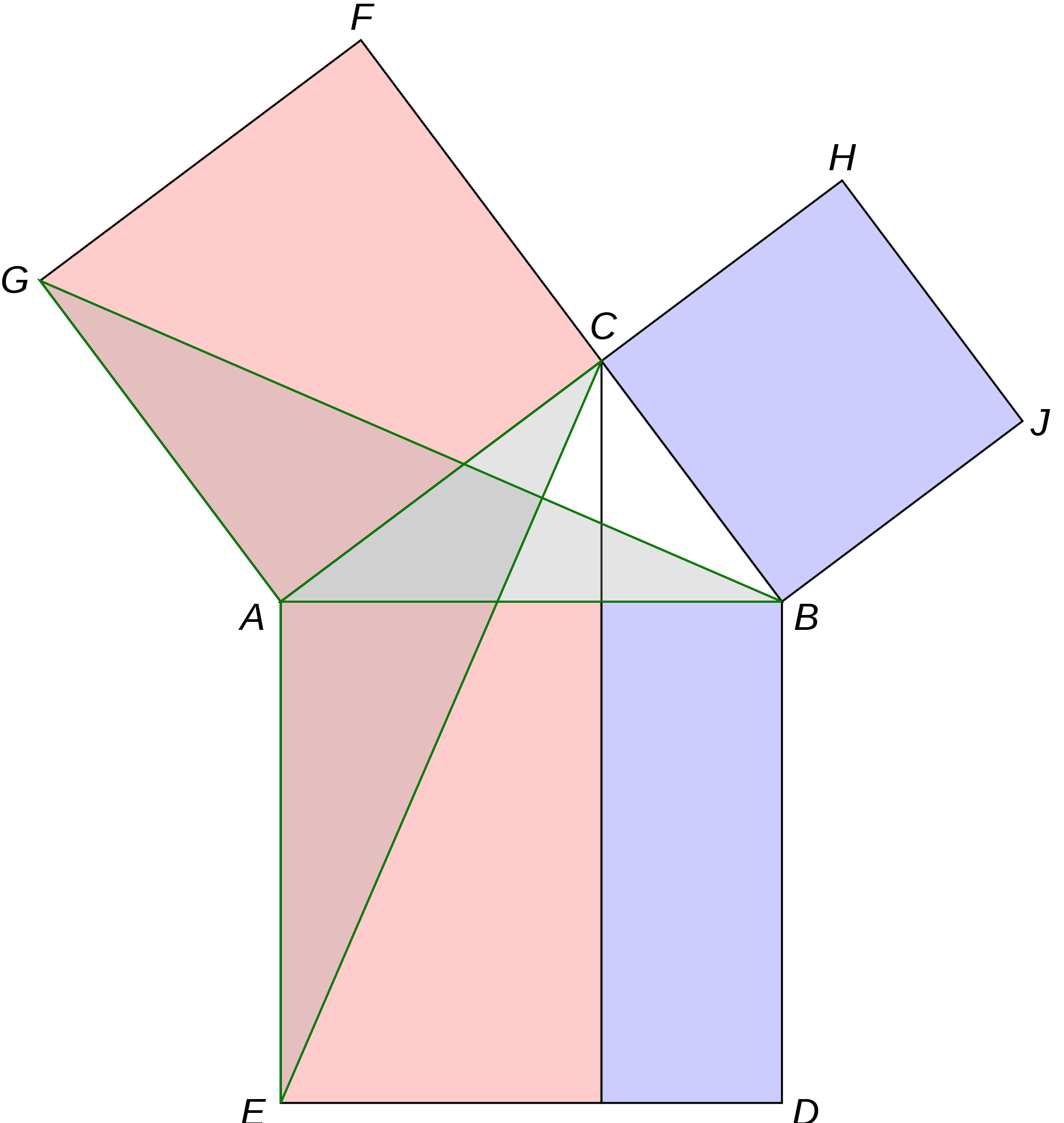
Pythagoras' Theorem has received at least 370 different proofs over the last 25 centuries, many of them Geometrical. This theorem, and its generalization into the Law of Cosines, are at the center of most Risk models

Similarly, Topology helps unveil the complex structure governing a system. The "Seven Bridges of Königsberg" problem inaugurated that field in Mathematics, when Euler recognized that understanding a system required modeling the logical and hierarchical interrelations between its components. While at Cornell University, Richard Feynman revolutionized nearly every aspect of theoretical physics thanks to his Topological approach to handling the morass of calculations involved in quantum electrodynamics (QED) problems.

The goal of my research is to forecast financial systems and make optimal decisions under uncertainty. In order to achieve that, I may apply probability theory, inferential statistics, vector spaces, stochastic calculus, etc. However, when possible, I prefer to state a problem Geometrically or Topologically, because it gives me the leverage to comprehend it before committing equations to a paper. For example, here is a Geometry work from Ronald Fisher dealing with Karl Pearson's (a Geometry professor at Gresham College) most famous invention: Correlation. Geometry is the right way to think about correlations. And when it comes to understanding complex dynamic systems with logical and hierarchical relationships, Topology is the way to go!

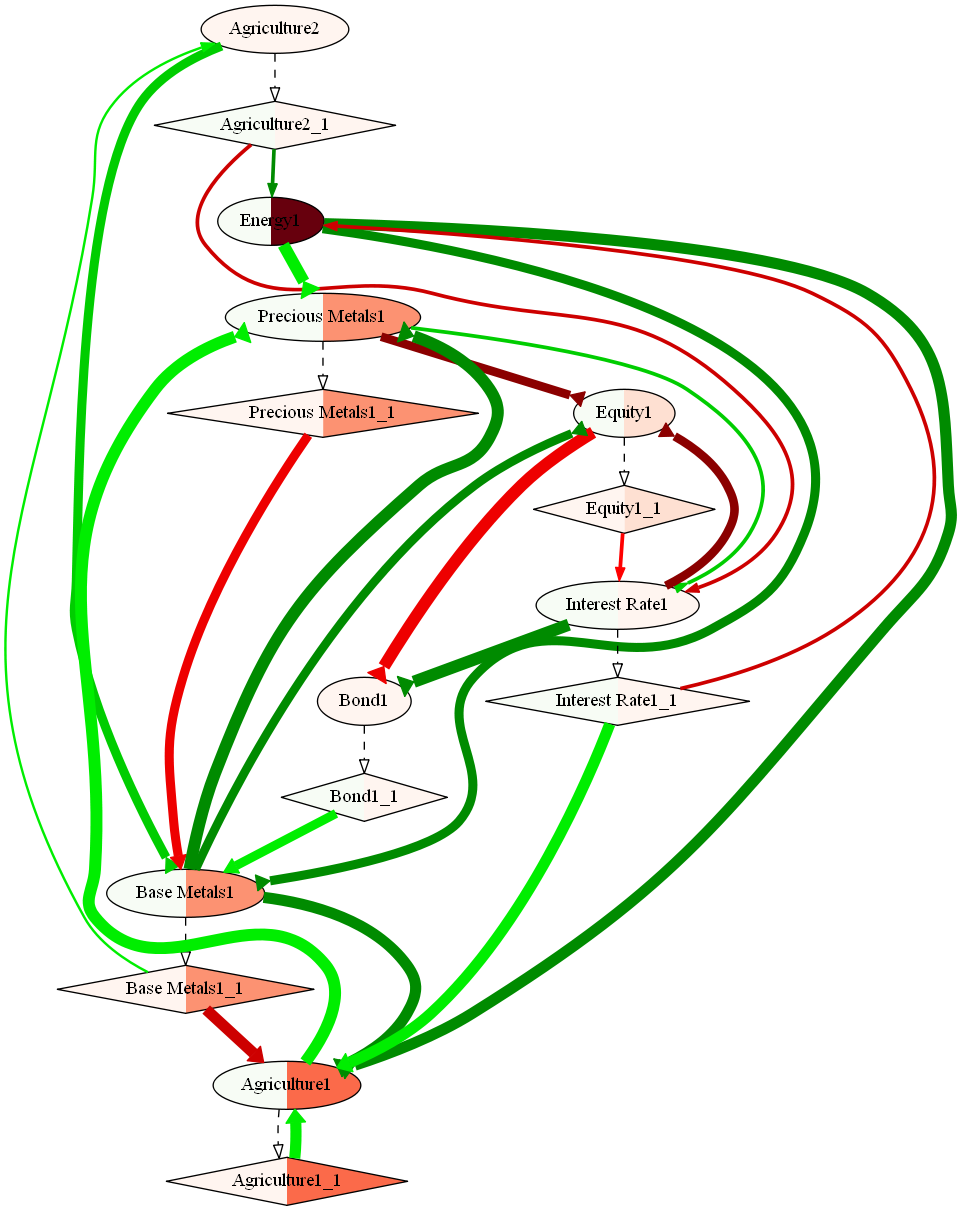
Financial markets are prime examples of complex dynamic networks: We can only understand the behavior of one price after modeling the dynamics of all prices. The above figure shows the Stochastic Flow Diagram of the global financial system, following an Energy shock

Academic genealogy studies how schools of thought are transmitted over generations, from advisors to doctoral students. Studying one's academic ancestry is partly an amusement, a tribute or a homage, however it can also explain how some of us came (consciously or unconsciously) to think about these problems Geometrically and Topologically. Mathematicians with shared academic ancestors are more likely to read each others' publications and eventually work together. The tables below show my line of doctoral advisors, which quickly converges from Mathematical Finance to Geometry and Topology (here is a chart according to the Math Genealogy Project).

Source: American Mathematical Society, Complutense University's Dissertations Catalogue, Spain's Ministry of Science and Royal Academy of Economic Science.

Source: American Mathematical Society, Complutense University's Dissertations Catalogue and Spain's Royal Academy of Sciences.

STUDENT	ADVISOR(S)	DISSERTATION	FIELD	YEAR	UNIVERSITY	COMMENTS
Julio Rey Pastor	Eduardo Torroja y Caballe; Felix Klein	Correspondence of Elemental Figures with application to their Derived Figures	Geometry	1909	Complutense University	Between 1911 and 1914, he studied at the University of Berlin and the University of Gottingen, under the supervision of Felix Klein. During that period, he also studied under the supervision of Professors Hermann Schwarz, Friedrich Hermann Schottky (father of Walter Schottky, Nobel Prize in Physics in 1911), and Ferdinand Georg Frobenius. Rey Pastor’s scientific work focused both on research, and textbooks and articles for the general public. They reflected the changes that were taking place in mathematics.
Felix Klein	Rudolf Lipschitz	Über die Transformation der allgemeinen Gleichung des zweiten Grades zwischen Linien-Koordinaten auf eine kanonische Form	Geometry	1868	University of Bonn	Klein's contributions spanned group theory, complex analysis, non-Euclidean geometry, and the connections between geometry and group theory. His 1872 Erlangen Program, which classified geometries by their underlying symmetry groups, was a hugely influential synthesis of much of the mathematics of the day.
Rudolf Lipschitz	Peter Gustav Dirichlet	Determinatio status magnetici viribus inducentibus commoti in ellipsoide	Geometry	1853	University of Berlin	While Lipschitz gave his name to the Lipschitz continuity condition, he worked in a broad range of areas. These included number theory, algebras with involution, mathematical analysis, differential geometry and classical mechanics.
Peter Gustav Dirichlet	Simeon Poisson; Joseph Fourier	Partial Results on Fermat's Last Theorem, Exponent 5	Number Theory	1827	University of Bonn (H.C.)	Dirichlet made deep contributions to number theory (including creating the field of analytic number theory), and to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a function.
Joseph Fourier	Joseph Louis Lagrange	Unknown	Analysis	c.1795	École Normale Supérieure	In 1795, Fourier was appointed to the École Normale Supérieure, and subsequently succeeded Joseph-Louis Lagrange at the École Polytechnique. He discovered the Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honor.
Joseph Louis Lagrange	Leonhard Euler		Analysis		Prussian Academy of Science	Lagrange did not receive a doctoral degree, however Euler played the role of mentor and advisor in his advanced studies. On the recommendation of Euler and d'Alembert, in 1766 Lagrange succeeded Euler as the director of mathematics at the Prussian Academy of Sciences in Berlin, where he stayed for over twenty years, producing a large body of work and winning several prizes of the French Academy of Sciences. Lagrange's treatise on analytic mechanics, written in Berlin and first published in 1788, offered the most comprehensive treatment of classical mechanics since Newton and formed a basis for the development of mathematical physics in the nineteenth century.
Leonhard Euler	Giambattista Beccaria	Dissertatio physica de sono	Physics	1726	University of Basel	Euler is considered to be the preeminent mathematician of the 18th century, and one of the greatest mathematicians to have ever lived. He is also one of the most prolific mathematicians ever, possibly second only to Paul Erdös: His collected works fill 60–80 quarto volumes. A statement attributed to Pierre-Simon Laplace expresses Euler's influence on mathematics: "Read Euler, read Euler, he is the master of us all."

Source: American Mathematical Society and Complutense University's Dissertations Catalogue.

STUDENT	ADVISOR(S)	DISSERTATION	FIELD	YEAR	UNIVERSITY	COMMENTS
Marcos López de Prado	Eva del Pozo	Advances in High Frequency Strategies	Mathematical Finance	2011	Complutense University	My second doctoral dissertation. My first dissertation (2003) dealt with portfolio optimization under non-normal and serially dependent returns, and was published in 2004. At that time I was Head of Quantitative Equity Research at UBS Wealth Management, and portfolio construction for Ultra-High-Net-Worth Individuals (>$US30m) was a critical question for the bank, requiring the proper modeling of hedge fund returns.
Eva del Pozo	Jose A. Gil Fana	Mathematical Models for Controlling Solvency in General Insurance Policies	Mathematical Finance	1997	Complutense University	Professor of Mathematical Finance (2008), and Vice-Dean of Quality Evaluation (2011) at Complutense's Business School. Her research focuses on the pricing of contingent claims in the general insurance business, of which financial options are a particular case.
Jose A. Gil Fana	Ubaldo Nieto de Alba	Mathematical Modelling of the General Insurance Business	Mathematical Finance	1983	Complutense University	Full professor of Mathematical Finance. Author of numerous textbooks and papers on contingent claims, operations research, insolvency forecasts, mathematical modeling of claim counts, etc.
Ubaldo Nieto de Alba	Angel Vegas Perez	Economic foundations in the Mathematics of Financial Operations	Mathematical Finance	1962	Complutense University	Dean of Complutense's Business School (1970-1973), Senator (1977-1982), President of the Senate's Finance Commission (1977-1982), President of the Government Acountability Office since 1982. Member of the Royal Academy of Economic Science since 1989. Order of Alfonso X the Wise.
Angel Vegas Perez	Miguel Vegas y Puebla-Collado; Julio Rey Pastor	A Survey of Mathematics Applied to Economic Studies	Mathematical Finance	1940	Complutense University	Prof. Vegas Perez was the son of the eminent mathematician, Prof. Miguel Vegas y Puebla-Collado. In the year 1948, he published the book A General Course of Mathematics Applied to Economics, which became the standard Mathematical Finance textbook used in Spanish-speaking Universities. Dean of Complutense's Business School (1968-1970), member of the United Nations Demographics Commission, Order of Merit of the Italian Republic, Order of Isabella the Catholic, etc. Member of the Royal Academy of Economic Science since 1982.

STUDENT	ADVISOR	DISSERTATION	FIELD	YEAR	UNIVERSITY	COMMENTS
Miguel Vegas y Puebla-Collado	Eduardo Torroja y Caballe	A Geometric Study of Third-Order Differentiable Curves	Geometry	1888	Complutense University	Prof. Vegas y Puebla-Collado's Analytic Geometry was an internationally acclaimed tractatus of Geometry, which followed the influences of Prof. Torroja, a disciple of Prof. Staudt. Member of the Royal Academy of Sciences since 1905.
Eduardo Torroja y Caballe	Karl Georg Christian von Staudt	On Staudt's Method of Projective Geometry	Geometry	1873	Complutense University	He obtained his Math degree from Complutense in 1864. Very early in his studies he became a disciple of Karl Georg Christian von Staudt, whose ideas of Geometry he embraced and promoted among his fellow mathematicians for the rest of his life. Member of the Royal Academy of Sciences since 1891.
Karl Georg Christian von Staudt	Carl Friedrich Gauss	On Ephemerides and the Orbits of Asteroids	Geometry	1822	University of Erlangen-Nuremberg	The book Geometrie der Lage (1847) was a landmark in projective geometry. Staudt went beyond real projective geometry and into complex projective space in his three volumes of Beiträge zur Geometrie der Lage published from 1856 to 1860. The Staudt-Clausen theorem is partially named after him.
Carl Friedrich Gauss	Johann Friedrich Pfaff	Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse	Algebraic Number Theory	1799	University of Helmstedt	Sometimes referred to as Princeps Mathematicorum. In his 1799 doctorate in absentia, A new proof of the theorem that every integral rational algebraic function of one variable can be resolved into real factors of the first or second degree, Gauss proved the Fundamental Theorem of Algebra. Mathematicians including d'Alembert had produced false proofs before him, and Gauss's dissertation contains a critique of d'Alembert's work. Ironically, by today's standard, Gauss's own attempt is not acceptable, owing to implicit use of the Jordan curve theorem. However, he subsequently produced three other proofs, the last one in 1849 being generally rigorous.